CS202: Discrete Structures Certification Exam Answers

Clear My Certification March 12, 2024 Computer Science Leave a comment 84 Views

Discrete structures refer to mathematical structures that deal with countable, distinct entities rather than continuous values. These structures are fundamental to computer science, mathematics, and various other fields. Some key areas of discrete structures include:

Set Theory: Sets are collections of distinct objects, and set theory provides the foundation for many other areas of mathematics. It deals with operations on sets, such as union, intersection, and complement, as well as concepts like subsets and power sets.
Graph Theory: Graphs consist of vertices (nodes) and edges (connections between nodes). Graph theory studies the properties of graphs, including connectivity, paths, cycles, and graph coloring. Graphs are widely used to model relationships in computer networks, social networks, and transportation systems.
Combinatorics: Combinatorics is the study of counting, arrangement, and combination of objects. It deals with problems like permutations, combinations, and the pigeonhole principle. Combinatorics has applications in cryptography, coding theory, and algorithm analysis.
Discrete Mathematics: Discrete mathematics is a broad field encompassing various discrete structures and techniques, including logic, number theory, and discrete probability. It provides tools for reasoning about discrete objects and is crucial in computer science for algorithm design, formal verification, and cryptography.
Boolean Algebra: Boolean algebra deals with operations on binary variables (true/false or 0/1) and logical expressions. It is fundamental to digital logic design and plays a crucial role in designing and analyzing digital circuits.
Relations and Functions: Relations describe associations between elements of sets, while functions are special kinds of relations that map elements from one set to another. Understanding relations and functions is essential in database theory, discrete optimization, and mathematical modeling.
Finite State Machines: Finite state machines (FSMs) are mathematical models used to represent the behavior of systems with a finite number of states. They are widely used in computer science for designing control circuits, parsing algorithms, and modeling sequential processes.

Understanding discrete structures is essential for various applications in computer science, including algorithm analysis, data structures, cryptography, artificial intelligence, and database management. It provides a solid mathematical foundation for solving complex problems and reasoning about discrete systems.

CS202: Discrete Structures Exam Quiz Answers

Question 1: Which of the following set pairs are equal sets? Select one:

X = {1, 3, 9, 7}; Y = {3, 1, 7}
X = {1, 3, 9, 7}; Y = {3, 1, 5, 9}
X = {1, 3, 9, 7}; Y = {3, 1, 7, 9}
X = {1, 3, 9, 7}; Y = {1, 3, 9, 7, 11}

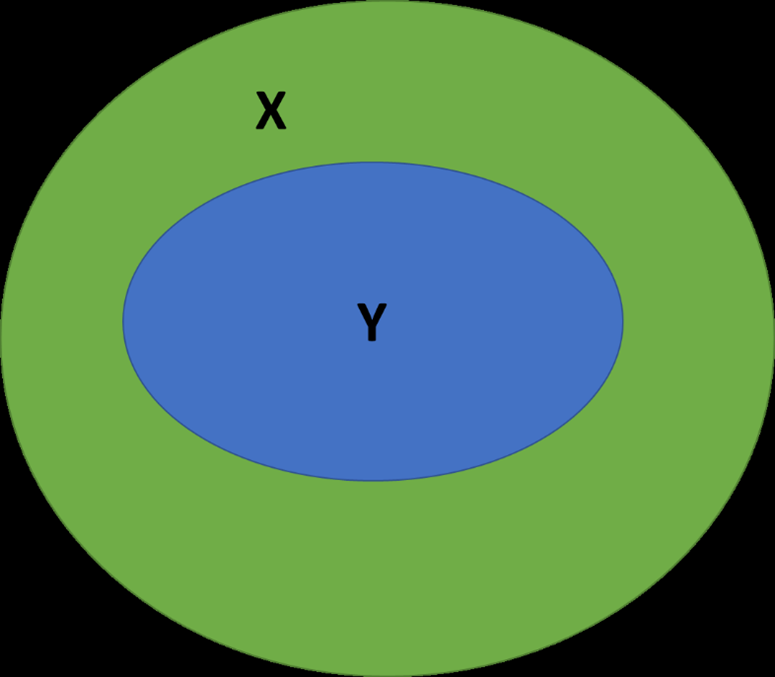
Question 2: Consider the sets X and Y in this figure. What type of set is Y?

Select one:

Y is equal to X
Y is a subset of X
Y is a superset of X
Y is equal to the null set

Question 3: Assume there are three sets: W, X, Y. What equation results in the intersection of those sets? Select one:

W – X – Y = Z
W ∪ X ∪ Y = Z
W ⋂ X ⋂ Y = Z
W ⊕ X ⊕ Y = Z

Question 4: Which of the following is (A − B) ∪ (A ∩ B) ∪ (B − A) equal to? Select one:

A
B
A ∪ B
The empty set

Question 5: Which of the following is the underlying assumption that is necessary for the Rule of Products to hold true? Select one:

Elements in set X depend on specific elements in set Y
Elements in set X must be independent of elements in set Y
Elements in set X must entirely overlap with elements in set Y
Elements in set X must be completely different from elements in set Y

Question 6: How many subsets does the set a, b, c�, �, � have? Select one:

Question 7: We would define the term “proposition” as a sentence that has which of the following qualities? Select one:

It can only meaningfully be called “completely true”
It can meaningfully be either “completely true” or “completely false”
It is “partially true”, where “partially” refers to some degree of truth
It is “partially false”, where “partially” refers to some degree of falsehood

Question 8: Consider the equation p → (p ∨ q). What is the result if both p and q are false? Select one:

True
False
Cannot be determined
This is not a logical proposition

Question 9: 3c.1. Assume that a system has three events (E1, E2, E3) that must take place before a fourth event, E4, can occur. Which of the following logical equations ensures the first three events take place before the fourth event? Select one:

E4 = E1 ^ E2 ^ E3
E4 = E1 v E2 v E3
E4 ⇔ E1 ⇔ E2 ⇔ E3
E4 = ᆨE1 ^ ᆨE2 ^ ᆨE3

Question 10: You have the following requirement: The computer’s run light (L) should come on when power (P) has been applied and the computer is ready to function (F), and when the computer’s start button (S) is pressed or data (D) begins to flow to the computer’s functioning input port (I). Which of the following logical equations would fulfill this requirement? Select one:

L = (P ^ F) ^ (S ^ (D ^ I))
L = (P ^ F) ^ (S ∨ (D ^ I))
L = (P ∨ F) ∨ (S ^ (D ∨ I))
L = (P ∨ F) ∨ (S ∨ (D ∨ I))

Question 11: If Mary helps Michael so that he gains new abilities that enable his task’s completion, and Michael uses his new abilities to help Susan so that Susan is successful, what role does Mary play in Susan’s success? Select one:

Mary has been enabled by Susan
Mary has been enabled by Michael
Mary has an implied role in Susan’s success
Mary has nothing to do with Susan’s success

Question 12: In an inductive proof of, ∀n P(n), n = 0, 1, 2, 3, …, …, …, n, …, which of the following is the base case? Select one:

Showing P (0)
Showing P(n)
Proving P(n-1) ⟹ P(n), n = 1, 2, 3, ….
Proving P(n) ⟹ P (n + 1), n ∈ ℕ, the natural numbers

Question 13: A new deck of playing cards has 52 cards. What is the probability that an ace is drawn on the second trial if a face card is drawn on the first trial and not placed back into the deck? Select one:

3/13
4/51
4/51
11/52

Question 14: On a 10-question true-or-false test, if you answer by flipping a coin, which of the following is P (getting a grade of 100%) the same as? Select one:

0
1/ (210)
1/10
½

Question 15: Consider a collection of independent events, each of which produces one of the following temperatures in a boiler {22, 23, 22, 24, 25, 30}. What is the probability that a temperature of 22 will occur, P(T₂₂)? Select one:

1/6
1/3
1/2
6/2

Question 16: Which of the following is an example of a recursive formula? Select one:

f(x) = 2x
f(y) = (2y) – 1
f(n) = f(n-1) + 1
P (A ∪ B) = P(A) + P(B), where A and B are disjoint and P is the probability function

Question 17: Given: f(x) = (5 * f(x-2)) − 3 ∀ x, f (2) = -3. What is the value of f (15)? Select one:

35,156
-58,593
-292,968
15 is not a member of the described sequence

Question 18: The structural integrity (s) of a building is known to decline by 0.2% per year. If s_{t, t ≥ 0} is the structural integrity of the building at t years after construction, write a recursive relation that is specific for s. Select one:

st = f(st-1)
st = 0.002 * st-1
st = 0.99998 * st-1
st = st-1 – 0.99998

Question 19: Which of the following is a graph composed of? Select one:

Edges and links
Vertices and edges
Vertices and nodes
Directional notations

Question 20: Which of the following best describes a Hamiltonian graph? Select one:

Any graph that contains a circuit
A graph with a path whose vertex list contains every vertex of the graph
A graph that contains a circuit, touching each edge of the circuit exactly once
A graph with a path whose vertex list contains each vertex of the graph exactly once

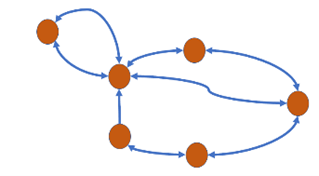
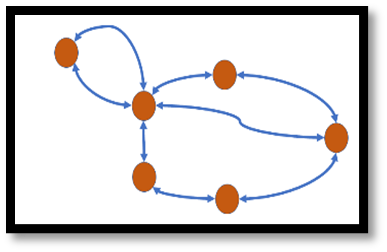
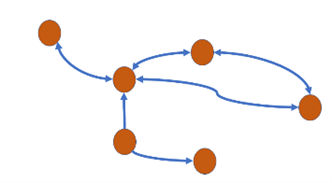
Question 21: Which of the following graphs is undirected? Select one:

Question 22: In this weighted directional graph, the weights give sensor values that cause the described system to go from one state to another.

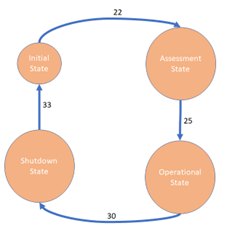
The sensor delivers these values:

Time	Sensor Value
0	0
1	2
2	20
3	25
4	26
5	27
6	30
7	31
8	31
9	32
10	33

What state is the system in after Time₁₀?

Select one:

Assessment State
Initial State
Operational State
Shutdown State

Question 23: Which of the following would be a way to illustrate a directed graph with this description?

Vertex List	Edge List
V1	{v1, v2}
V2	{v2, v1}
V3	{v2, v3}
V4	{v3, v4}
	{v4, v3}
	{v4, v1}

Select one:

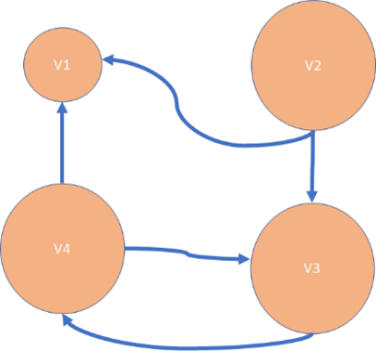
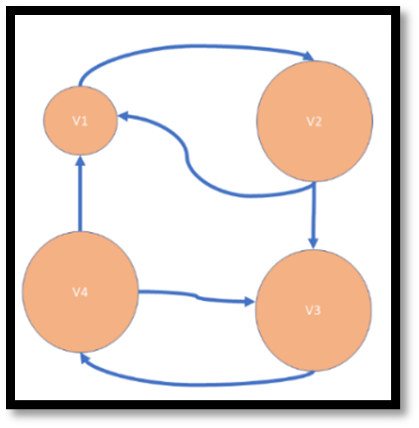
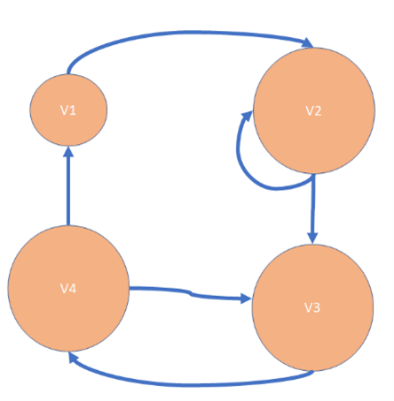
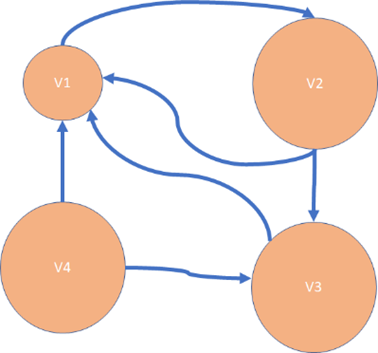
Question 24: Which of the following graphs is a tree? Select one:

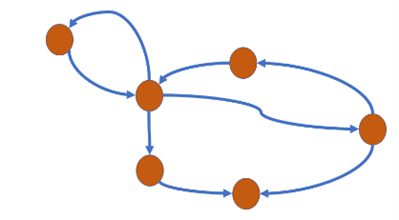
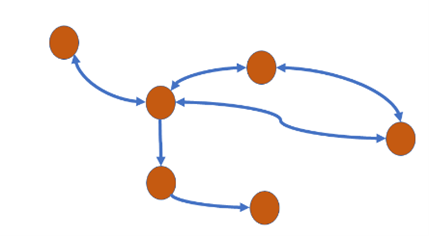
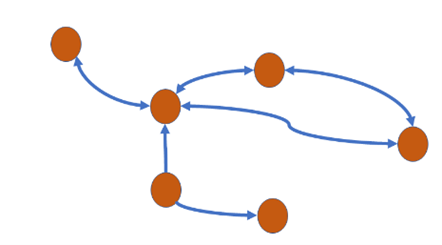
Question 25: Which of the following characteristics describes a binary tree? Select one:

There are only two cycles
There are only two subtrees
Each vertex has one or more subtrees
Each vertex has no more than two subtrees

Question 26: Which of the following descriptions would be a good explanation of what the system in this image does?

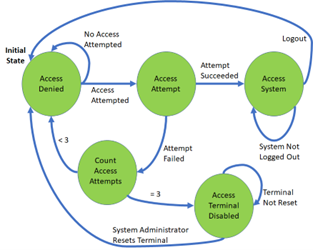
Select one:

A system terminal is active. It remains active until logout. Upon successful login, the system is accessible until logout.
A system terminal sits idle. It remains idle until login is attempted. Two failed login attempts are allowed. The third causes the terminal to become disabled. Reset by a system administrator is then required for the terminal to be re-enabled. Upon successful login, the system is accessible until logout.
A system terminal sits idle. It remains idle until login is attempted. Two failed login attempts are allowed. The third causes the terminal to become disabled. Automatic reset then occurs after five minutes so that the terminal is re-enabled. Upon successful login, the system is accessible until logout.
A system administrator enables an access terminal. The terminal then sits idle until login is attempted. Two failed login attempts are allowed. The third causes the terminal to become disabled. Reset by a system administrator is then required for the terminal to be re-enabled. Upon successful login, the system is accessible until logout.

Question 27: Which of the following are the essential rules for constructing state diagrams for a system that can only be in one state at a time? Select one:

There can be multiple transitions specified for a given state data input or external action impacting the state; and for every data input or external action impacting a state, a transition specification must exist
There can be only one transition specified for a given state data input or external action impacting the state; and for every data input or external action impacting a state, a transition specification must exist
There can be multiple transitions specified for a given state data input or external action impacting the state; and for every data input or external action impacting a state, a transition specification need not exist since the system is assumed to remain in its present state until a transition event occurs
There can be only one transition specified for a given state data input or external action impacting the state; and for every data input or external action impacting a state, a transition specification need not exist since the system is assumed to remain in its present state until a transition event occurs

Question 28: What is the maximum size of a set? Select one:

Finite
Infinite
A countable number of elements
Not countable, but also not infinite

Question 29: Which of the following is this statement an example of?

If x in A implies x in B and x ∉ B, then x ∉ A. Select one:

Resolution
Modus Tollens
Modus Ponens
Conjunctive specialization

Question 30: Imagine there exists a network of ten computers. These computers can work independently on specific tasks. Tasks are assigned to them by another computer on that same network. There are many ways such a network can be employed. The case at issue involves cameras that capture visual events and transmit the resulting pictures to a receiving computer. That computer assigns pictures to other networked computers for analysis. The analysis of one picture has nothing to do with the analysis of any other picture. If 100 pictures are suddenly sent by the cameras, in how many ways can these pictures be assigned to the analysis computers? Select one:

10101010
1010010100
1001010010
100!90!

Question 31: Consider this truth table. What does it tell us?

p�	q�	p∧q�∧�
0	0	0
0	1	0
1	0	0
1	1	1

Select one:

If any fact is true then the conclusion is true
The conclusion is true only when all facts are true
A conclusion can be chosen at random regardless of the facts
The conclusion is true when all facts are true or when no facts are true

Question 32: Consider the logical equation X = (A ^ ¬B) ∨ (C ^ D). What is the result if A, B, C, D are all true? Select one:

True
False
The result is logically incongruent
Sheffer Stroke of (A ∪ B) and (C ∪ D)

Question 33: How might we calculate the probability of an event? Select one:

Set it equal to the probability of the just-prior causal event
Divide the probabilities of the string of causal events into each other
Add the probabilities of the individual outcomes that lead up to the event
Multiply the probabilities of the individual outcomes that lead up to the event

Question 34: What is the mathematical definition of an independent event? Select one:

P(A∩B) = P(A) ⋅ P(B)
P(A∩B) = P(A) + P(B)
P(A∩B) = P(A) / P(B)
P(A∩B) = P(A) – P(B)

Question 35: What is the difference between a directed graph and an undirected graph? Select one:

An undirected graph can be traversed in exactly one direction
A directed graph can be traversed in any direction from any node
An undirected graph can be traversed in any direction from any node
A directed graph has only one circuit with a traversal path is specified by directional notation

Question 36: Two separate state machines exist, M1 and M2. M2 takes input from M1. However, M1 operates independently from M2. If M1 has a number of states equal to S1 and M2 has a number of states equal to S2, how many possible state combinations could be achieved? Select one:

S12
S22
S1 + S2
S2 * S1

Question 37: Consider the set W, X, Y, Z in this figure. What operation on sets W, X, Y gives us set Z?

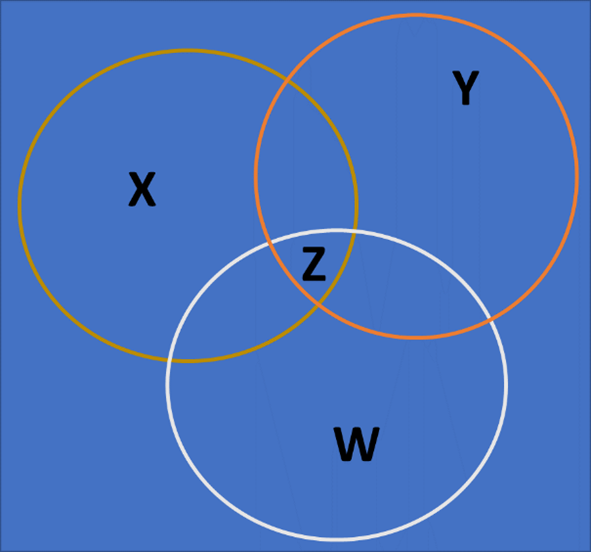
Select one:

Union of W, X, Y
Intersection of W, X, Y
W, X, Y are subtracted from each other
W, X, Y are subtracted from the universal set

Question 38: Which of the following can be said about all possible outcomes of a random experiment? Select one:

They cannot be stated, and what will happen cannot be predicted
They can be stated, and the probability of all possible outcomes lies along a uniform distribution
They can be stated, but the actual outcome on any given trial cannot be predicted with any certainty
They can be stated, and the actual outcome on any given trial can be predicted within a specified probability

Question 39: An eCommerce company pays a popular website to display an advertisement for a specific product. Of the 100 customers visiting the product’s website during the ad campaign, only 60 had seen the advertisement. Of the 40 customers purchasing the product, 30 had seen the ad. What is the probability that a visiting customer saw the ad and purchased the product? Select one:

25%
30%
50%
60%

Question 40: Why would any application want so many paths between nodes?

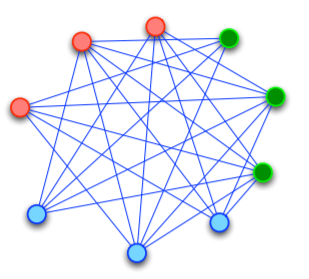
Select one:

A fully-connected graph is necessary for traversal
The design consumes appears sophisticated and is likely to be accepted
Physical traversal requires multiple paths should a given path fail or be bottlenecked
Application owners can charge for the additional computer time needed to determine the shortest path

Question 41: Which of the following is a binary tree? Select one:

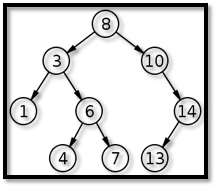
Question 42: Consider sets X and Y in this figure, and assume those are the only sets under consideration. Which of the following equations leaves only the green part of set X?

Select one:

X = Ø
Y ↔️ X
Y ⟶ X
X = ⇁Y

Question 43: Which of the following is this statement an example of?

Given x in A ∩ B, it follows that x in A. Select one:

Resolution
Specialization
Generalization
Modus Ponens

Question 44: If there are A elements in set X and we wish to group them in sets having (A−b) non-repeating elements, what formula do we use? Assume that X has no repeating elements. Select one:

AA−b
(A−b)!
P (A, A−b)
(A/A−b)

Question 45: 3c.2. Assume that a system has three events (E1, E2, E3). One of these must take place before a fourth event, E4, can occur. Which of the following logical equations ensures one of the first three events take place before the fourth event?

Select one:

E4 = E1 ^ E2 ^ E3
E4 = E1 v E2 v E3
E4 ⊕ E1 ⊕ E2 ⊕ E3
E4 = ᆨE1 v ᆨE2 v ᆨE3

Question 46: What is the negation of this equation?

¬ (A ^ B ∨ ¬C ∨ ¬D) Select one:

¬A ∨ ¬B ^ C ^ D
¬A ^ ¬B ∨ C ∨ D
A ^ B ∨ ¬C ∨ ¬D
¬A ^ ¬B ∨ ¬C ∨ ¬D

Question 47: If P(x) is True for x in C, Q(x) is True for x in D, and P(x) => Q(x), then which of the following is accurate? Select one:

C is a subset of D
D is a subset of C
For some x in D, P(x)
There exists an x in D

Question 48: If it is true that (a → b → c → … → z), which of the following might be a simple way to state an obvious conclusion? Select one:

a → z
a ⇔ z
a ⇒ z
a ⇏ z

Question 49: If we wish to prove that (q0 → q1, q1 → q2, …, qn−1 → qn, qn → qn+1, q0 ⇒ qn+1) is true, what type of reasoning could we employ? Select one:

Analogy
Deductive
Inductive
Reductive

Question 50: In the entertainment industry, customers generally enjoy variety. A producer has a choice between five acts. Three of the acts are aerial and two are magical. Each type of act has one all-female group. If a show is to feature a female act chosen at random, what is the chance that the act will be magical? Select one:

20%
40%
50%
60%

Question 51: 6b.2. If the Fibonacci Sequence is defined as Fk = Fk−2 + Fk−1 for k ≥ 2, is this a complete specification? Why? Select one:

No; you must also know the value of Fk for k = 0
No; you must also know the value of Fk for k = 1 and k = 2
Yes; the recursive sequence resolves itself as it proceeds
Yes; you know everything you need to perform the calculation

Question 52: If an integer n is in N, the set of natural numbers, how would we specify the Kth previous number in the set regardless of the value of n? Select one:

n + K, n ≥ 0
n + 1, n ≥ 0
n – K, n ≥ 0
n – k, n ≥ K

Question 53: Assume we have a mathematical model composed of Gaussian equations (G) centered at different points along a line. The purpose of the model is to predict the value of the next sample as data streams through the model {D1, D2, D3, …}. The prediction of the value of the next data sample is based on the error of the previous prediction and the value of the now-current data sample. What would be a broad and recursive expression for the prediction component of this model? Error is referred to as E, Data as D, and Predicted Value as P. Select one:

P = E*G(D)
Pt = Et*G(Dt)
Pt+1 = Et-1*G(Dt)
Pt+1 = Et-1*G(Dt-1)

Question 54: What is the difference between a graph and a tree? Select one:

A tree has no circular paths
A tree cannot be fully traversed
A tree enables direct access to all nodes
A tree has only one subgraph that contains a cycle

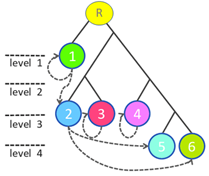
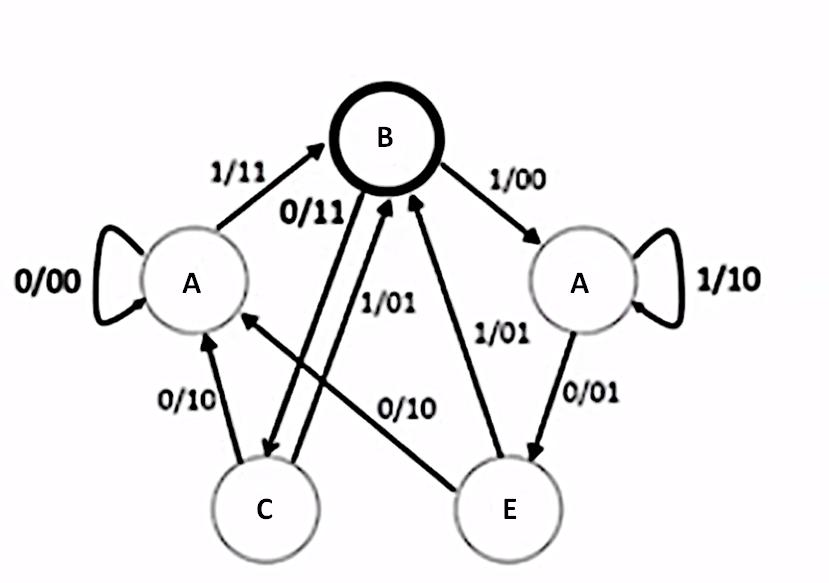
Question 55: Using this truth table, which of the following correctly labels the states in this figure? Note that x/y for a transition state means that output value y is achieved for input value x.

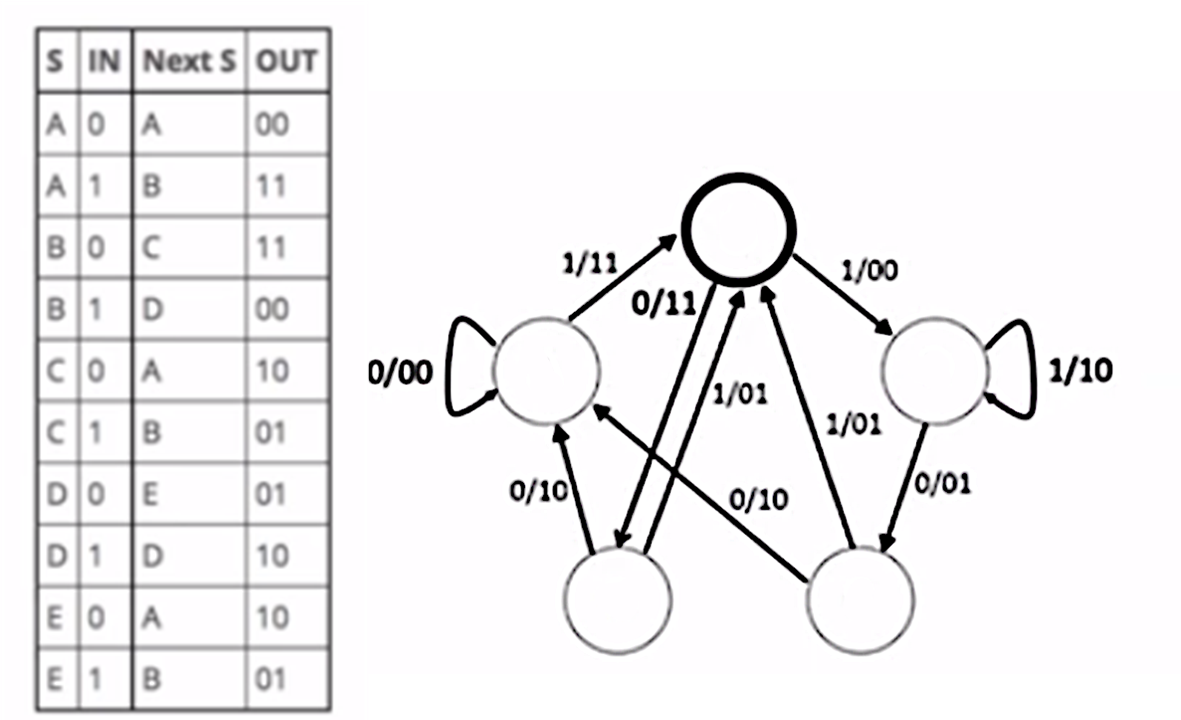
Select one:

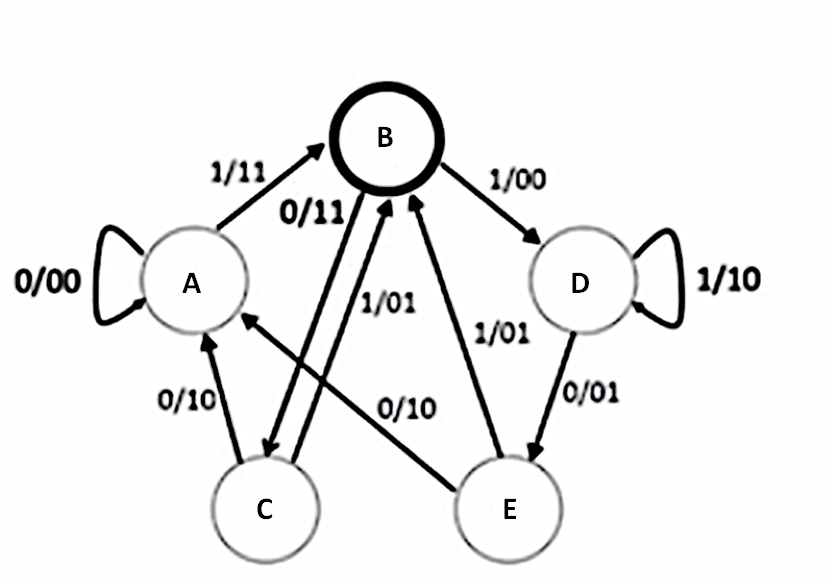
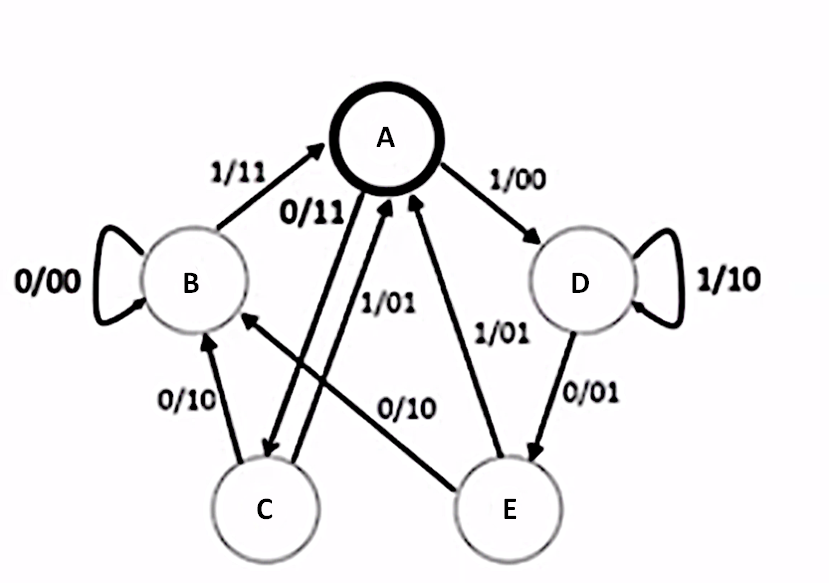
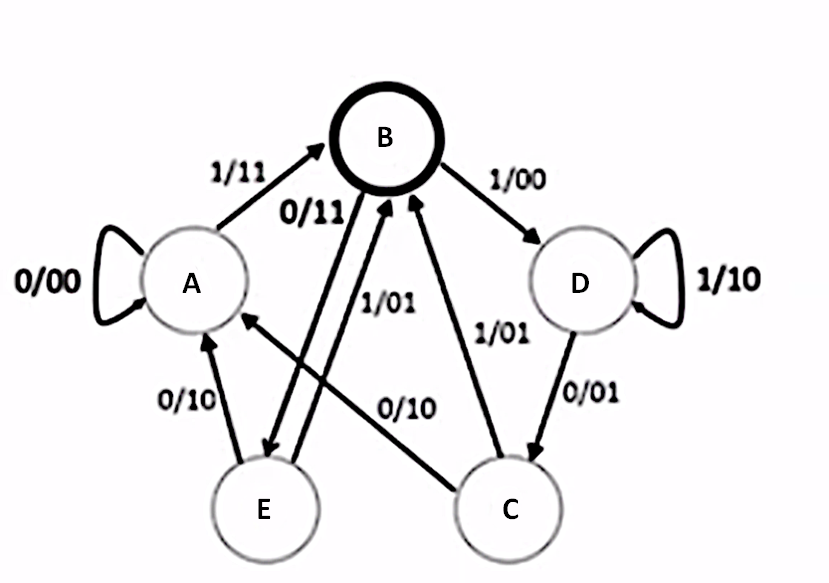
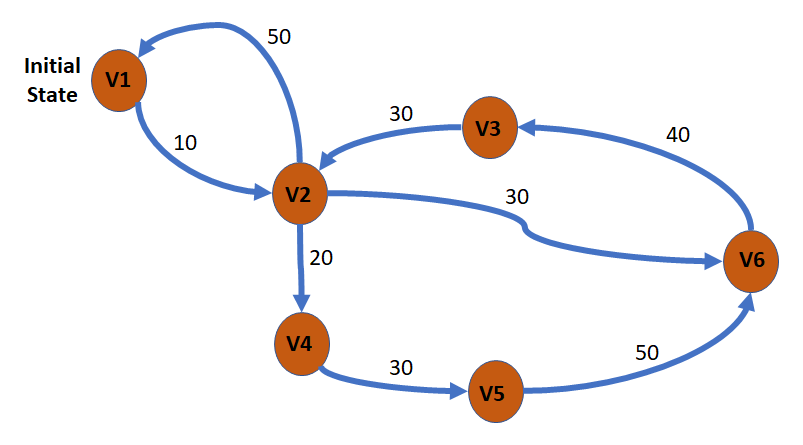
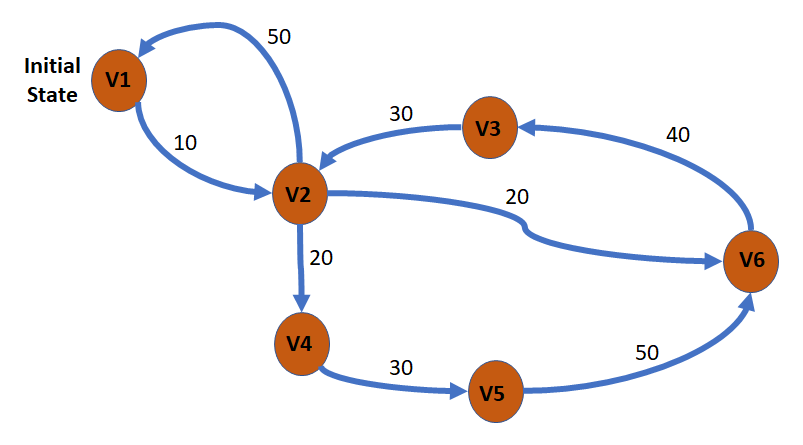
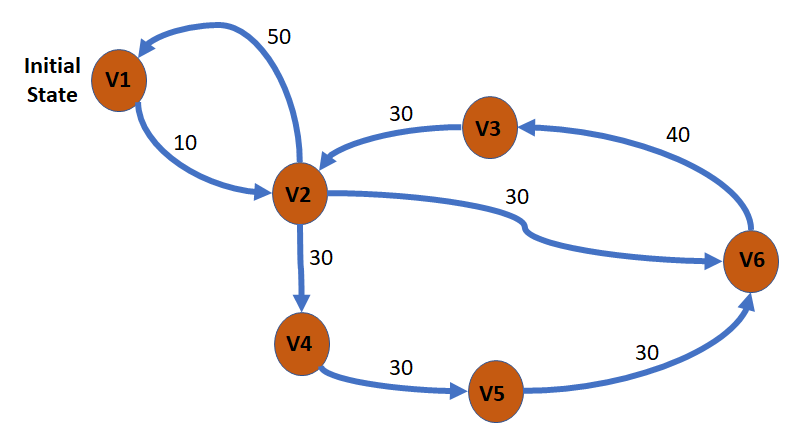
Question 56: Which of the following system illustrations can be in only one state at a time? Note that the system changes state only when the given transition values are reached. Select one:

Question 57: Which of the following is correct, using true/false logic? Select one:

1 + 1 = 0
1 + 1 = 1
1 + 1 = 2
1 + 1 = 10

Question 58: Which of the following is this statement an example of?

Given x > 1, it follows that x > 0.

Select one:

Conjunctive specialization
Disjunctive specialization
Elimination
Resolution

Question 59: How do simple induction and strong induction differ? Select one:

They have different base cases
They have different inductive steps
They require different levels of proof
They have different inductive assumptions

Question 60: A recursive mathematical function is a mathematical function f(a, b, …) that has which of the following properties? Select one:

Uses far less memory than its explicit version
Can be calculated once the values of (a, b, c…) are known
Defines none of its input parameter values (a, b, …) in terms related to those same parameter values
Defines some or all of its input parameter values (a, b, …) in terms related to those same parameter values

Question 61: Which of the following best describes a spanning tree? Select one:

A tree within a connected graph that connects all nodes of the graph
A subgraph of a connected graph that is a tree connecting all nodes of the graph
A subgraph of a connected graph that connects all nodes of the graph with a minimum number of edges
A subgraph of a connected graph that is a tree connecting all nodes of the graph with a minimum number of edges

Question 62: Which of the following is this statement an example of?

Given x in A ∪ B’ and x in C ∪ B, it follows that x in A ∪ C.

Select one:

Resolution
Elimination
Disjunctive specialization
Conjunctive specialization

Question 63: If every vertex of a graph has a distance ≤ 4 from a given vertex v, what is the diameter of the graph? Select one:

4
8
≥ 4
≥ 8

Question 64: An Eulerian graph is a graph that does which of the following? Select one:

Contains a circuit that touches every edge of the graph exactly once
Contains one or more circuits that touching each edge of the circuit exactly once
Contains a circuit that contains most edges of the graph, touching each only once
Has no circuits, and the graph can be traversed by touching every vertex exactly once

Question 65: What are the basic components of a tree? Select one:

Vertices, edges, edges with or without direction
Nodes, links, edges without direction, no cycles
Nodes, links, edges with or without direction, no cycles
Nodes, links, edges with direction, only one cyclic subtree

Question 66: Which of the following statements about trees and graphs is true? Select one:

A graph is a tree
A tree is a graph
A graph is directed
A tree can have a loop

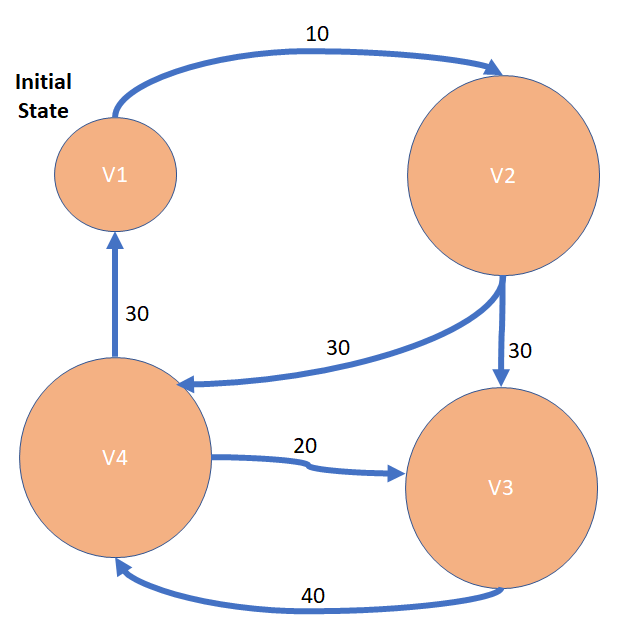
Question 67: A special notation shows directional connections between graph vertices and the sensor data required to move from one vertex (system state) to another. For instance, {V1, V2, S} shows the sensor data value required to move from vertex V1 to vertex V2. Which of the following descriptions indicates a system that can be in exactly one of a finite number of states at any given time?

Select one:

Origin State	Target State	Sensor Data Value
V1	V2	10
V2	V4	30
V2	V3	30
V3	V4	40
V4	V3	20
V4	V1	30

Origin State	Target State	Sensor Data Value
V1	V2	10
V2	V1	50
V2	V6	30
V6	V3	40
V3	V2	30
V2	V4	30
V4	V5	30
V5	V6	50

Origin State	Target State	Sensor Data Value
V1	V2	10
V2	V1	50
V2	V6	30
V6	V3	40
V3	V2	30
V2	V4	30
V4	V5	30
V5	V6	50

Origin State	Target State	Sensor Data Value
V1	V2	10
V2	V1	50
V2	V6	30
V6	V3	40
V3	V2	30
V2	V4	20
V4	V5	30
V5	V6	50

Question 68: Consider this situation: The main valve is closed when time equals six and the computer is waiting for another instruction, or when the computer is first initialized. What is the valve’s state when time equals five and the computer is waiting for another instruction, and the computer is ten seconds past its initialization phase? Select one:

The valve is closed
The valve is not closed
The valve remains in its present state
The valve will alternate between open and closed

Question 69: How could the series for 12, 22, 32, …, n2, … and k0, k1, k2, …, kn, …, be solved when k is a constant? Select one:

By deduction on n for both series
By induction on n for the first series and induction on k for the second series
By induction on n2 for the first series and induction on kn for the second series
By induction on n for the first series and induction on both k and n for the second series

Question 70: Conditional probability is given symbolically as P(A|B). Which of the following is the expansion of this rule? Select one:

P(A)/P(B)
P(A∪B)/P(B)
P(A∩B)/P(A)
P(A∩B)/P(B)

Question 71: A random number generator draws integers from a uniform distribution defined on the range 1…100. A seed is selected and then two sets of numbers are sequentially generated: S1 = {2, 16}, S2 = {37, 99, 41, 2}. Considering these two sets only, what can be said about S1 and S2? Select one:

S1 and S2 are independent
S1 and S2 are not independent
S1 and S2 were generated using a weak seed
S1 and S2 were generated using a strong seed

Question 72: The binomial coefficient (nk) is how we write “the number of groups attained if n objects are partitioned into unique groups having k unique members”. If we specify the recursive version of the calculation as (nk)=(n−1k) +(n−1k−1) if n>k>0, what is missing in the specification? Select one: